- 反復的アルゴリズム
- ループ
目次
再帰的アルゴリズムの3原則
- 終了条件をもつ
- 毎回状態を変え、終了条件に近づく
- それ自身を再帰的に呼び出す
再帰的アルゴリズムの例:数の階乗
- 5! = 5 × 4× 3× 2× 1 (cf. 50 = 1)
参考)反復的アルゴリズムで書くと
- 6行で書ける
def factorial(n):
the_product = 1
while n > 0:
the_product *= n
n = n - 1
return the_product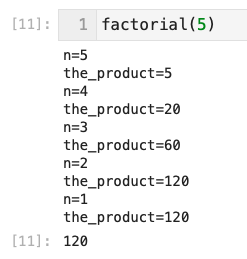
再帰的アルゴリズムで書くと
if n == 0 return 1が終了条件- 終了条件に当てはまらなければ、
return n * factorical(n - 1)のコードが実行される - 4行で書ける
- 再掲↓

def factorical(n):
if n == 0: # 終了条件
return 1
return n * factorical(n - 1)中身がどう動いているのか?
- 毎回関数が
returnに到達するたびに、スタックに中間結果を記憶する - スタックはリストのようなもの
- ただし、追加した順番どおりに要素が取り除かれる
- たとえば、以下の場合
factorical(3)
# n = 3 → 2 → 1 → 0- Pythonは、
n * factorical(n-1)をまだ計算できないため、状態を内部スタックに保存する - 5行目の戻り値が
factorical(0)(n=0)となって、はじめてif n == 0: return 1の終了条件が満たされるため、1が返ってくる。
# 内部スタックの状態
[ return n * factorical(n-1), # n = 3 この状態ではまだ計算ができない
return n * factorical(n-1), # n = 2 〃
return n * factorical(n-1), # n = 1 〃
return 1 ] # n = 0 計算できた。計算後は内部スタックから除外される- ここで、最後の結果1を使って、それ以前の計算をできるようになる!
- またその結果を内部スタックから取り除いていく
# 内部スタックの状態
[ return n * factorical(n-1), # n = 3
return n * factorical(n-1), # n = 2
1 × 1 = 1] , # n = 1 計算後は内部スタックから除外される# 内部スタックの状態
[ return n * factorical(n-1), # n = 3
2 × 1 = 2] , # n = 2 計算後は内部スタックから除外される# 内部スタックの状態
[ 3 × 2 = 6 ] # 結果6が返ってくる再帰をいつ使うのか?
- 再帰をどのくらいの頻度で使うかは自分次第
- 再帰的に書けるすべてのアルゴリズムは、反復的(ループ)でも書ける
- 再帰のメリット
- 少ない行で済むこと(洗練されている)
- 再帰のデメリット
- メモリーを使ってしまうこと(内部スタックに保存する必要があるため)
- 反復的アルゴリズム(再帰よりメモリーは少ない)で書いた場合より、何が起こっているかのトレースが難しい
TODO:漸化式を使うらしいが、、、よくわからない