- 並び替えをする場合、様々なソートアルゴリズムがあるが、それぞれに長所と短所がある
- ある種のソートアルゴリズムは、イテラブルが大体ソートされているといった特定の状況で、とても有効
- イテラブルとは「繰り返し可能なオブジェクト」のこと(ex.リスト、タプル、など)
- この章では、バブルソート、挿入ソート、マージソートを扱う
- このほかにもクイックソート、シェルソート、ヒープソートなどがある
- 実際にプログラムを実装する場合は、プログラミング言語に組み込まれたソート関数を使うこと
- 理由:古典的なものに比べて高速だから
- 章で学ぶものは古典的なもの
- じゃあ、ここでなぜ学ぶのか?
- 時間計算量についての理解が深まるため
- ソートの仕組みなどのように、ソート以外の場面で使える概念の理解に役立つ
目次
用語集
- バブルソート
- 任意の数字のリストに対して、隣接する2つの文字を比較し、順番になっていない場合はそれらの交換を繰り返し実行するアルゴリズム
- 安定ソート
- 最初の並びを保持するソートの種類
- 挿入ソート
- 手札に持つトランプのカードを並び替えるようにデータを整列させるアルゴリズム
- マージソート
- 要素が1つだけ含まれるサブリストになるまでリストを半分ずつ分け続け、その後、正しい並び順に整列しながら統合していく再帰的なアルゴリズム
- 分割統治法
- 再帰的に問題を2つ以上の関連した小さな問題に分割していき、各問題が簡単に解けるようなサイズにして、問題を解く手法
- ハイブリッドソートアルゴリズム
- 2つ以上の同じ問題を解けるアルゴリムを組み合わせることで、扱うデータに応じて、どのアルゴリムを使うかを適切に切り替えながら処理するアルゴリム
バブルソート
- 5行目:loop_size – i の「- i」は最初の繰り返し実行時に、リストの一番右側と比較が不要なため(7行目で比較して入れ替わっているため)。-iがなくても問題なく回るが効率が悪い
- 行4,8,9のswapは、並び順の変更がなければ、そのリストの並び順はすでに整っており、もうそれ以上の処理が必要ないための処理。
def bubble_sort(a_list):
loop_size = len(a_list) - 1
for i in range(loop_size):
no_swap = True #
for j in range(loop_size-i):
if a_list[j] > a_list[j+1]:
a_list[j], a_list[j+1] = a_list[j+1], a_list[j]
no_swap = False
if no_swap:
return a_list
return a_list
a_list = [1, 6, 9, 32, 50]
バブルソートをいつ使うのか?
- バブルソートは、数字の並び順を昇順に変える。また文字列の並びを変えるようなバブルソートを書くことも出来る
- バブルソートの大きな長所は、非常にシンプルに実装できること
- そのため、ソートアルゴリズムを学ぶのにちょうどよい出発点になる
- バブルソートは2つのforを使った入れ子のループになるため、時間計算量は
O(n2) - 膨大なデータ量では使えないため、学習用で学ぶ以外にバブルソートを使うことはない
- バブルソートは安定ソート(並び替えが行われる前の並びを保持している)
挿入ソート
- 手札にもつカードを並び替えるようにデータを整列させるアルゴリム
- 2つ目の数字からカードを1枚ずつ見て、数字の大きいカードを小さいカードよりも右側へ挿入していくイメージ
- ポイントは、最初にa_list[i]のvalueの値を保持し、その間にそれより左側の値a_list[i-1]が大きければ、a_list[i]の場所に上書き。iを1つだけ戻した後、a_list[i-1]の場所にvalueを戻す点
def insection_sort(a_list):
for i in range(1, len(a_list)):
value = a_list[i]
while i > 0 and a_list[i-1] > value:
a_list[i] = a_list[i-1]
i = i - 1
a_list[i] = value
return a_list
a_list = [6, 5, 8, 2]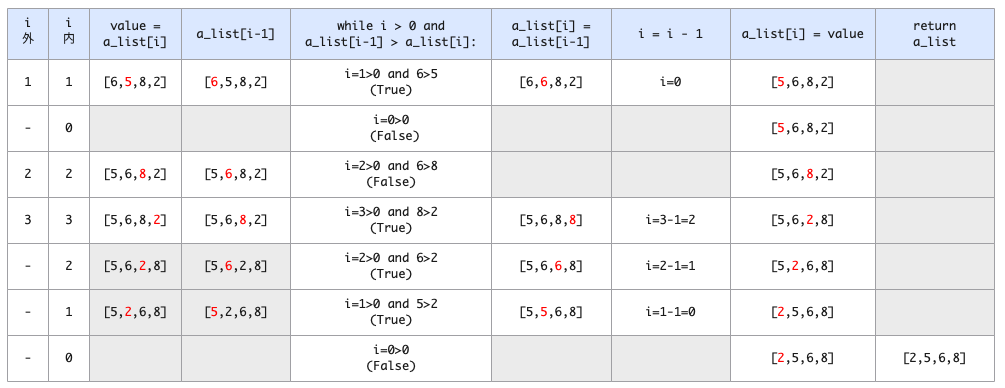
挿入ソートをいつ使うのか
- バブルソートと同じで、挿入ソートは安定ソート
- 時間計算量も同じ
O(n2)で、効率的でないが、バブルソートと異なり挿入ソートは実務で使える - 挿入ソートは、ほとんど並び替えの終わっているデータがある場合に使える
- リストがすでに整列されていたり、ほぼ整列されている場合には、時間計算量は
O(n)となり、とても効率的なアルゴリズムになる - たとえば、[1, 2, 3, 4, 5, 7, 6]リストをソートする場合、5までは上記スクリプト行4の条件を満たさないため、Whileループに入らずにすむ
マージソート
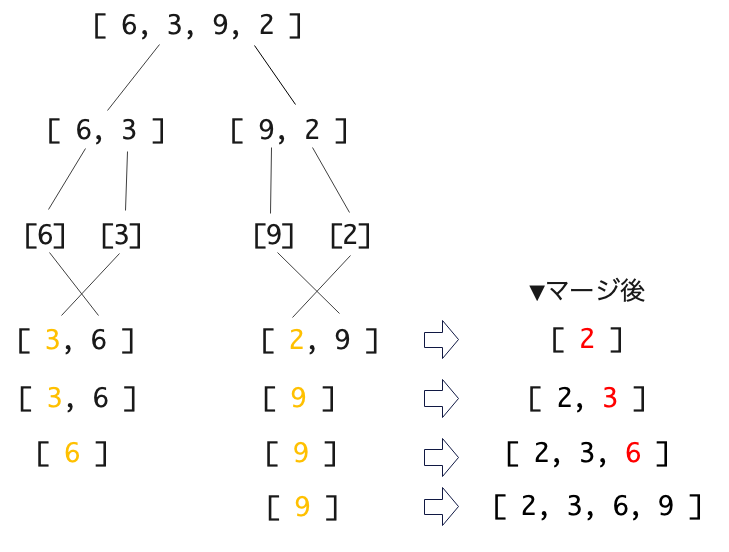
- 要素がひとつだけ含まれるリストになるまで、リストを半分ずつに分け続け、その後、正しい並び順に整列しながら統合していく再帰的なアルゴリズム
def merge_sort(a_list):
# リストを再帰的にサブリストに分割
if len(a_list) > 1:
mid = len(a_list) // 2
left = a_list[:mid]
right = a_list[mid:]
merge_sort(left)
merge_sort(right)
# 2つのリストをマージする
left_i = 0
right_i = 0
alist_i = 0
while (left_i < len(left)) and (right_i < len(right)):
if left[left_i] <= right[right_i]:
a_list[alist_i] = left[left_i]
left_i += 1
else:
a_list[alist_i] = right[right_i]
right_i += 1
alist_i += 1
# leftとrightにまだ残っている要素があればa_listにマージする
while left_i < len(left):
a_list[alist_i] = left[left_i]
left_i += 1
alist_i += 1
while right_i < len(right):
a_list[alist_i] = right[right_i]
right_i += 1
alist_i += 1
return a_list- 実行結果
==================================================
TOP:a_list=[6, 12, 13, 9, 10]
left=[6, 12]
right=[13, 9, 10]
--------------------------------------------------
==================================================
TOP:a_list=[6, 12]
left=[6]
right=[12]
--------------------------------------------------
==================================================
TOP:a_list=[6]
==================================================
TOP:a_list=[12]
■ while①:(left_i=0 < len(left)=1) and (right_i=0 < len(right)=1)
True
>if条件:left[left_i]=6 <= right[right_i]=12
True
● a_list[0]<---left[left_i]=6
a_list=[6, 12]
left_i=1,right_i=0,alist_i=0
left_i=1,right_i=0,alist_i=1
■ while③
● a_list[1]<---right[right_i]=12
a_list=[6, 12]
left_i=1,right_i=1,alist_i=2
==================================================
TOP:a_list=[13, 9, 10]
left=[13]
right=[9, 10]
--------------------------------------------------
==================================================
TOP:a_list=[13]
==================================================
TOP:a_list=[9, 10]
left=[9]
right=[10]
--------------------------------------------------
==================================================
TOP:a_list=[9]
==================================================
TOP:a_list=[10]
■ while①:(left_i=0 < len(left)=1) and (right_i=0 < len(right)=1)
True
>if条件:left[left_i]=9 <= right[right_i]=10
True
● a_list[0]<---left[left_i]=9
a_list=[9, 10]
left_i=1,right_i=0,alist_i=0
left_i=1,right_i=0,alist_i=1
■ while③
● a_list[1]<---right[right_i]=10
a_list=[9, 10]
left_i=1,right_i=1,alist_i=2
■ while①:(left_i=0 < len(left)=1) and (right_i=0 < len(right)=2)
True
False
★a_list[0]<---right[right_i]=9
a_list=[9, 9, 10]
left_i=0,right_i=1,alist_i=0
left_i=0,right_i=1,alist_i=1
■ while①:(left_i=0 < len(left)=1) and (right_i=1 < len(right)=2)
True
False
★a_list[1]<---right[right_i]=10
a_list=[9, 10, 10]
left_i=0,right_i=2,alist_i=1
left_i=0,right_i=2,alist_i=2
■ while②
● a_list[2]<---left[left_i]=13
a_list=[9, 10, 13]
left_i=1,right_i=2,alist_i=3
■ while①:(left_i=0 < len(left)=2) and (right_i=0 < len(right)=3)
True
>if条件:left[left_i]=6 <= right[right_i]=9
True
● a_list[0]<---left[left_i]=6
a_list=[6, 12, 13, 9, 10]
left_i=1,right_i=0,alist_i=0
left_i=1,right_i=0,alist_i=1
■ while①:(left_i=1 < len(left)=2) and (right_i=0 < len(right)=3)
True
False
★a_list[1]<---right[right_i]=9
a_list=[6, 9, 13, 9, 10]
left_i=1,right_i=1,alist_i=1
left_i=1,right_i=1,alist_i=2
■ while①:(left_i=1 < len(left)=2) and (right_i=1 < len(right)=3)
True
False
★a_list[2]<---right[right_i]=10
a_list=[6, 9, 10, 9, 10]
left_i=1,right_i=2,alist_i=2
left_i=1,right_i=2,alist_i=3
■ while①:(left_i=1 < len(left)=2) and (right_i=2 < len(right)=3)
True
>if条件:left[left_i]=12 <= right[right_i]=13
True
● a_list[3]<---left[left_i]=12
a_list=[6, 9, 10, 12, 10]
left_i=2,right_i=2,alist_i=3
left_i=2,right_i=2,alist_i=4
■ while③
● a_list[4]<---right[right_i]=13
a_list=[6, 9, 10, 12, 13]
left_i=2,right_i=3,alist_i=5
[233]:
[6, 9, 10, 12, 13]マージソートをいつ使うのか
- マージソートは、分割統治法の例の一つ
- 分割統治法とは、問題を再帰的に2つ以上の関連した小さな問題に分割していき、各問題が解けるようなサイズにして、問題を解く手法
- マージソートでは、リストを要素数が1つになるまで、サブリストに分割していく
- 要素が1つだけのサブリストはソート済みと見なすので、マージしていくのは簡単
- マージソートは、対数線形時間量
O(n log n) - これは与えられたリストをサブリストに分割するのは対数時間計算量
(n)が必要なため - 対数時間計算量であるため、マージソートはもっとも効率的なソートアルゴリズムの一つであり、広く活用されている
- たとえば、Pythonの組み込みのソートアルゴリズムに、このマージソートを使っている
- マージソートは安定ソート(バブルソートや挿入ソートと同様)
- 例えば、教室に50人の学生がいて、全員がポケットに100以下の小銭をいくらかもっているとする
- 学生が持っている小銭の総額を知る一番良い方法は?
- 最初に思いつくのは、先生がクラス中を歩いて、一人ずつ回収して総額を計算する方法。この場合、線形探索のため時間計算量は
O(n) - もう一つは、全学生それぞれが隣の学生とペアになり、横の学生の小銭を集め合算する
- 小銭のなくなった学生は部屋を退出する。教室に学生が1人になるまでこの作業を繰り返す
- この方法だと6ステップで総額がわかる
Pythonにおけるソートアルゴリズム
- Python には、
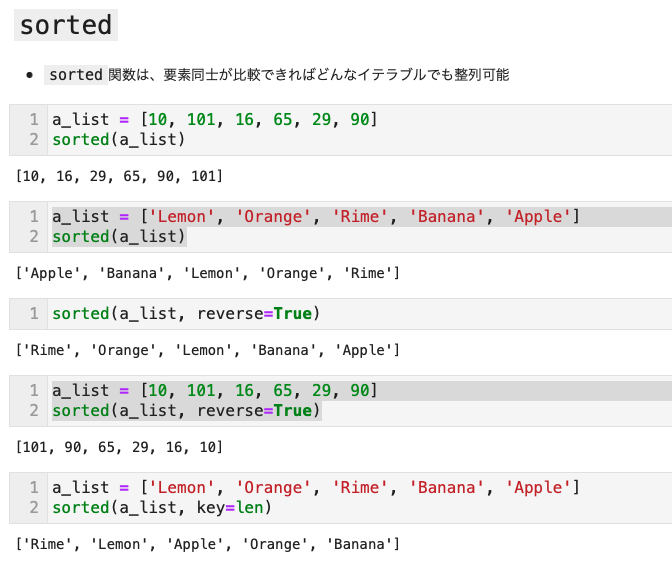
listのsortメソッド と - イテラブルをソートできる
sorted組み込み関数がある - それらのソート関数は、
Timsortという、マージソートと挿入ソートを足し合わせたソートアルゴリズ(ハイブリッドソートアルゴリズム)を使っている - ハイブリッドソートアルゴリズムは、2つ以上の同じ問題を解けるアルゴリズムを組み合わせることで、扱うデータに応じて、どのアルゴリズムを使うかを適切に切り替えながら処理するアルゴリズム
- 挿入ソートとマージソートのハイブリッドである
Timesortは、非常に効率的なアルゴリズム - よほどのことがないかぎりは、自分でソートアルゴリズムを実装せずに、Python標準を使ったほうがよい
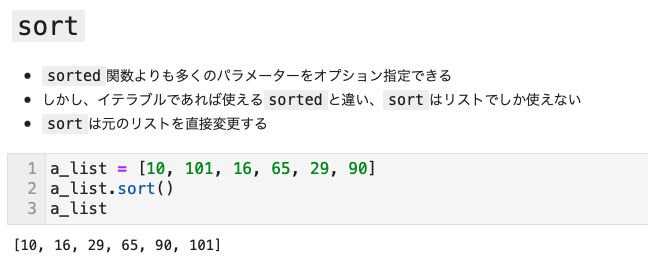
- ~.sort() の場合、戻り値はNoneになるため、変数に格納できない