第6章数学 – note to self

用語集

記数法
　数を数字で表す方法。1つの桁に何個の数字がでてくるか、ってこと。
基数
　記数法が使うアラビア数字の数。例）基数が10の場合、10進数で0から9までのアラビア数字を指す
2進数
　基数を2とした記数法
ビット
　2進数における桁数のこと。binary digitが語源
位の値
　数字の位置によって変わってくる数量のこと。10進数では、1452は千が1つ、百が4つ、十が5つ、一が2つあることを表す数字
ビット演算子
　2つの数値をビット単位で計算する演算子
最大公約数
　2つ以上の正の整数（自然数）に共通な約数（公約数）のうち、最大の約数のこと
境界条件
　プログラムが受け取る入力値の想定範囲を超えたとき、プログラムがどのように振る舞うか、に関する鵜条件や決めごと
素数
　2以上の正の整数で、正の約数がそれ自身と1のみの数

2進数

ビット演算子

プログラミングで数値を扱う場合、100や10.5といったintやfloatを使う
それでも、2進数で処理したほうが良い場合がある
たとえば、数字が2のべき乗かどうかを判断する場合、2進数が役に立つ
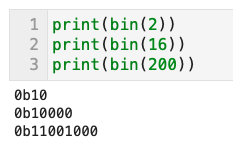
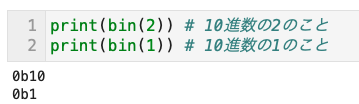
bin関数で数字を2進数に変換できる
先頭の「0b」は2進数をあらわす

# bin関数で数字を2進数に変換できる
bin(16)
>>'0b10000' <-- 先頭の「0b」は2進数をあらわす

ビット演算子は、2つの数値をビット単位で計算する算術演算子
算術演算子を説明するために、まず論理演算子の動作を確認する

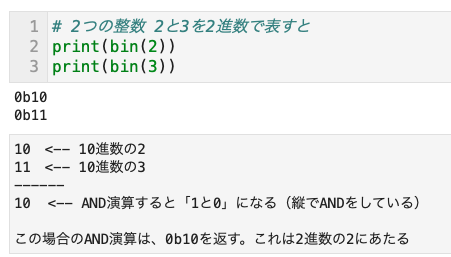
Pythonでは、ビットごとのAND演算は「&」を使う
これは2進数の桁（ビット）ごとにBoolean演算をおこなう
比較している2つの数の各桁ごとに値を比較し、どちらも1（True）のとき、PythonはTrueをかえす
そうでないときは、Falseをかえす

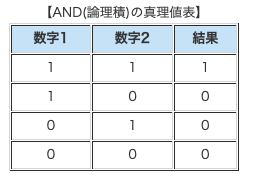
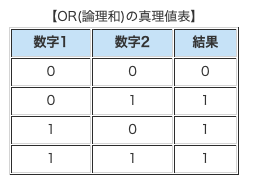
AND演算（論理積）とOR演算もある（論理和）

ビット演算子が役に立つケース

ビットごとのAND演算子を使うと、整数が「奇数か偶数か」をテストできる

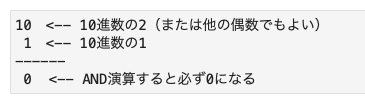
2などの偶数は、最下位の桁が0になっている

一方、1は利用価値が高い数字です
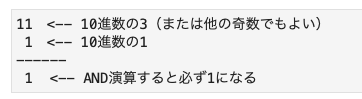
1は、2進数で表しても1になる。常に桁が1つです。次の2つの2進数をみてみよう

偶数（最下位の桁が0）と1とのAND演算では、Pythonは常にFalseを返す
これは、偶数は2進数では最下位の桁が必ず0、1は2進数でも1だけで、最下位の桁の値が異なるため

逆に、奇数（最下位の桁が1）と1とのAND演算では、常にTrueを返す

つまり、こういうことか？

再掲だが、1は2進数でも常に1桁というのは、とても意義がある
奇数か偶数かを調べる数値が何桁であろうと、1は常に1桁しかないため、右端の1桁だけビット演算すれば済む
Pythonでは以下のようにして、AND演算子を使って奇数（odd）か偶数（even）かをテストする

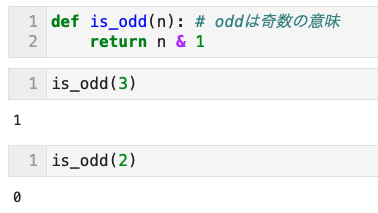
上記のis_odd関数では、n & 1 の結果を返す。n & 1 は、n と 1ビットごとのAND演算をおこなう
奇数と1でAND演算：Trueを返す（1、奇数）

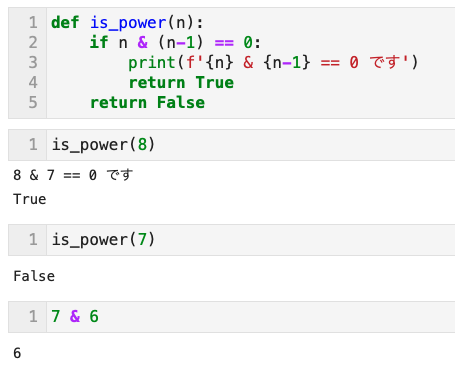
ビットごとのAND演算子を使って、整数が2のべき乗かどうかの判定も出来る

特徴1：

これは2のべき乗であるすべての整数は、2進数で表現したとき、1つだけしか1を含まない特徴を利用できる（2の倍数だから、何乗しても偶数だよね。。。）
たとえば、次の通り1つしか1が含まれてない

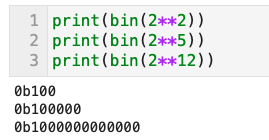
特徴2：

ここに2のべき乗のもう一つの特徴を組み合わせる
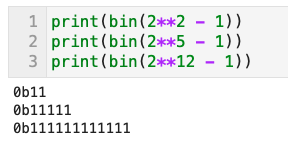
2のべき乗の整数から1を引いた値は、2進数ではすべての桁が1になる、といった特徴をつかう
例）

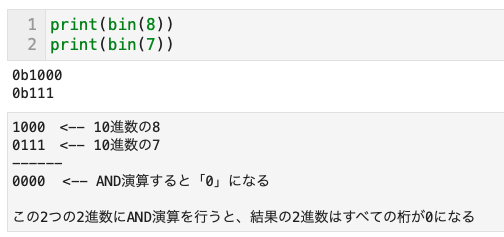
この2つの2進数にAND演算を行うと、結果の2進数は、すべての桁が0になる
- 注意）特徴1と特徴2の2進数の桁数は違う（2のべき乗が、2のべき乗-1より桁数は多い）
- 例）100 <–> 11、100000 <–> 11111

これらを何に使うのであろう。。。

FizzBuzz問題

問題：

数字の1から100までを出力してください
もし3の倍数なら、「Fizz」と出力
もし5の倍数なら、「Buzz」と出力
もし3と5の公倍数なら、「FizzBuzz」と出力してください

とくにむずかしくないが、この問題の鍵は、剰余演算子（モジュロ演算子）をうまく活用すること
剰余演算子とは、ある数を別の数で割り、その余りを返す演算子

どんなときに使えるか？というと

5万行もある文書ファイルがあるとする。1ページには49行しか収まらないとする。最後のページは何行になるか？
- 500000 % 49 = 20行が答え
他にも、2万レコードが入っているデータベースががある。全レコードでなく、1レコードおきごとに処理を入れたい場合
- 全レコード分で繰返しながら、偶数のときだけ処理を行う、など

最大公約数

最大公約数とは、2つかそれ以上の整数を割り切れる正の整数のうち、もっとも大きな数のこと

例）以下の最大公約数は4

20の約数：1, 2, 4, 5, 10, 20

12の約数：1, 2, 3, 4, 6, 12

def gcf(i1, i2):
    gcf_value = None
    if i1 > i2:
        smaller = i2
    else:
        smaller = i1
    for divisor in range(1, smaller+1):
        if (i1 % divisor == 0) and (i2 % divisor == 0):
            gcf_value = divisor
    return gcf_value

gcf(20,12)
>> 4

ただし、上記のプログラムは、入力する数字のどちらかが0だと、間違った答えを返す
そのため、この問題に対処が必要
このように、0の場合にどのように処理すべきかを決めておくことを境界条件とよぶ
最大公約数を計算する場合、もし片方の整数が0ならば、もう一つの整数が最大公約数になる
例）0と12の最大公約数は12
以下書き換えたもの

def gcf(i1, i2):
    if i1 == 0:
        return i2
    if i2 == 0:
        return i1
    
    if i1 > i2:
        smaller = i2
    else:
        smaller = i1
        
    for divisor in range(1, smaller+1):
        if (i1 % divisor == 0) and (i2 % divisor == 0):
            gcf_value = divisor
            
    return gcf_value

print(gcf(0, 12))
>>12

またこのプログラムは、負の数を処理できないため、追加の境界条件が必要

def gcf(i1, i2):
    if i1 < 0 or i2 < 0:
        raise ValueError('テストできる数は正の数だけ')
        
    # あとは同様

最大公約数のプログラムはnステップで解くため、時間計算量は線形でそれほど悪くはない
しかし、もっとよい方法がある。次で。

ユークリッドの互除法

最大公約数を探すためのより効率的な解法が、ユークリッドの互除法
最初に、2つの数の大きいほうの数 x を、もう一つの小さいほうの数 y で割り、その余りを求める
次に、求めた余りを、今度は割る数（除数）として扱い、もう一度割る
このとき、先ほどの y を割られる数（今回の割り算におけるx ）として扱う
この手順を繰返しし、余りが0になったときに使った、割った数（除数）が最大公約数

＜例：20と12の最大公約数を見つける＞

最初に、20を12で割る。余りは8
次に、12を8で割る。余りは4
次に、8を4で割る。余りは0
余りがないので、最大公約数は4

20 % 12 = 8
12 % 8 = 4
8 % 4 = 0

def gcf(x, y):
    if y == 0: # 境界条件
        (x, y) = (y, x)
    while y != 0:
        (x, y) = (y, x % y)
    return x

gcf(20, 12)

# x:y = 12:8
# x:y = 8:4
# x:y = 4:0
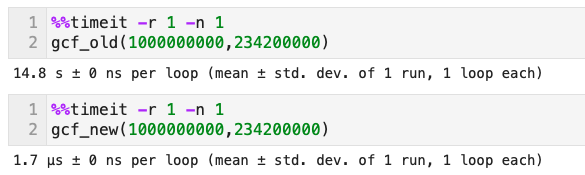
>> 4

このユークリッド互除法のアルゴリズムでは、時間計算量が、前の線形ではなく、対数になる
よって大きな数の最大公約数を見つける場合は、このアルゴリムを使うと飛躍的に処理速度が向上する
以下の速度を比較すると明らか（old：前の式、new:ユークリッド互除法）

素数

素数は2以上の正の整数で、正の約数がそれ自身と1のみの数のこと（例：2,3,5,7,11など）
ここでは、数 n が素数か否かを判断する関数の書き方を学ぶ
たとえば、n=3は素数。その約数は1と3=nのみ。どんな数値であっても1は約数になる
つまり、1とnを除く数で割りきれたら、それは素数ではないということ

def is_prime(n):
    for i in range(2, n):
        if n % i == 0:
            return False
    return True

print(is_prime(11))
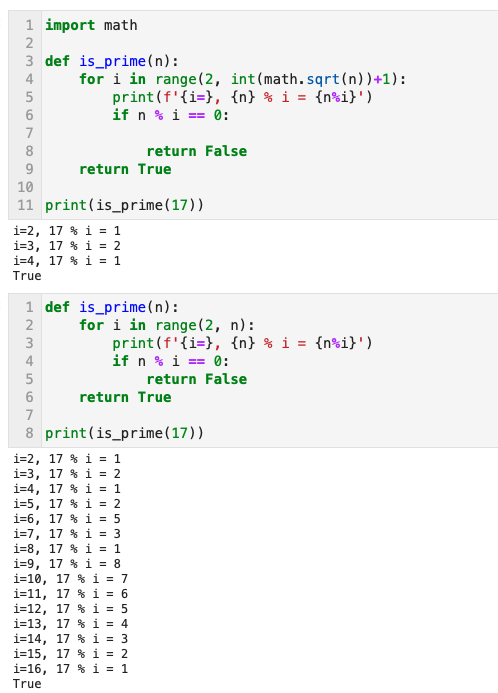
>> True

このアルゴリムは終わるまでn-2ステップ続くので、時間計算量は線形です
ループを、n-2ステップの代わりに、n の平方根でやめることで、処理時間を改善できる
n の平方根でステップをやめても良い理由は
もし、a * b == n なら、a か b は n の平方根と同じかそれ以下になる。
なぜかというと
a と b の両方とも n の平方根よりも大きい数だと、a * b は n よりも大きくなってしまい
n とは同じにはならない。
つまり、かけ算をしたときに n となる n の平方根よりも両方とも大きい a と b という数字は存在しない
割る数の1つが n の平方根よりも小さくないといけないので、n までテストする必要がないということ
その代わりに、n の平方根よりも1つだけ大きい整数でステップをやめてよいことになる
n を余りなしで割ることのできる n の平方根と同じかそれ以下の数が見つからない場合は、それ以上の大きな数でも n を余りなしで割れる数は存在しない

import math

def is_prime(n):
    for i in range(2, int(math.sqrt(n))+1):
        if n % i == 0:
            return False
    return True

print(is_prime(11))

nの平方根でやめた場合（上）と通常（下）の場合
- 下は i=5〜のループが無駄

指定する任意の数値範囲の素数リストを出力したい場合

def is_prime(n):
    for i in range(2, int(math.sqrt(n)+1)):
        if n % i == 0:
            return False
    return True

def find_primes(n):
    return [i for i in range(2, n) if is_prime(i)]
                   
print(find_primes(50))
>>[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31