- データの探索方法は、データを扱うプログラマーが知っておくべきもっとも基礎的な知識の一つ
- 自分で作成する必要はない。Python標準の探索アルゴリズムを使ったほうがよい
- じゃあ、なぜ探索アルゴリズムの書き方を学ぶのか?
- 線形や対数のオーダーといったコンピューターサイエンスの基本的な概念を理解する助けになるから
- またPython標準の探索アルゴリズムの中から、データセットにとってどれが効率が良いか判断するためには、これらのアルゴリズムを理解することが重要だから
目次
用語集
- 探索アルゴリズム
- データセットからデータを探すアルゴリズム
- データセット
- データの集合
- 線形探索
- データセットの各要素を繰り返し、探索対象と比較する探索アルゴリズム
- 二分探索
- リストから数値を探索するもう1つのアルゴリズムで、線形探索より高速
- 切り捨て除算演算子
- 割り算したときの商の、小数点以下の値を切り捨てた整数値を返す演算子
- べき乗
bn(Pythonではb**2)と書く数値演算。
- 底
bnのbのこと
- 指数
bnのnのこと
- 対数
- ある数値を別の数値にするために、何乗したらよいかの指数
- 文字コード
- 文字と2進数のマッピング
線形探索
- 線形探索では、データセットの「全要素」について繰り返し、探索対象と比較する
- 比較して一致すれば、その数値はリストにある
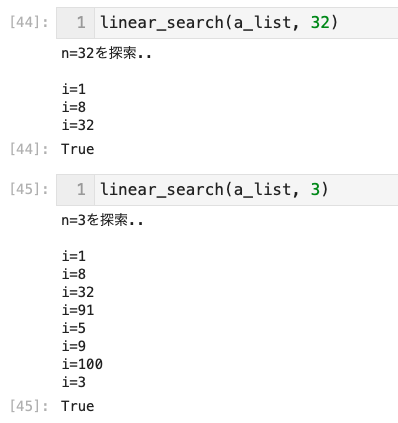
def linear_search(a_list, n):
print(f'{n=}を探索..','\n')
for i in a_list:
print(f'{i=}')
if i == n:
return True
return False
a_list = [1, 8, 32, 91, 5, 9, 100, 3]- 見つかるまで、全要素を1つずつ探索する
- リストの最初ごろに見つかればよいが、後の方だと見つかるまで1つずつ探索する必要がある
線形探索をいつ使うのか
- 線形探索のオーダーは
O(n)- リストが10つの場合、最良で
O(1)、最悪でO(10)になる
- リストが10つの場合、最良で
- 検索対象がソート済みでない場合は、線形探索をおすすめする
- 線形探索を使用したい場合は、Pythonの組み込みキーワードの
inを利用する(たった1行)
unsorted = [1, 45, 4, 32, 3]
print(45 in unsorted_list)
>> True- 文字列中の文字を探す場合は
print('a' in 'apple')
>> True二分探索
- リストから数値を探すための、より高速なアルゴリズム
- ただし、かならずデータセットがソート済みのときにだけ利用する
- リスト内の要素を半分に分割して探索する
def binary_search(a_list, n):
first = 0
last = len(a_list) - 1
while last >= first:
mid = (first + last) // 2
if a_list[mid] == n:
return True
else:
if n < a_list[mid]:
last = mid -1
else:
first = mid + 1
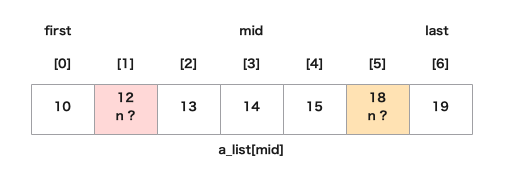
return False- たとえば、以下のリストを昇順に並び替えて18(または12)を探索しているとする
- まず中央値(a_list[mid])を見つける(ここでは14になる)
- 14は探しているnではないため、firstの位置をmid + 1 に設定しなおす(リスト前半を除外する)
- それを繰り返し、見つからなければリストにnはない
2分探索は線形探索よりかなり速い
- ループ1、繰り返し1の速度比較ではあるが
- 1秒=百万マイクロ秒だが。。。相当速い
二分探索をいつ使うのか
- 二分探索のオーダーは
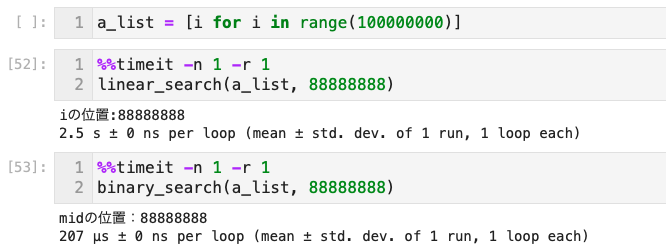
O(log n) - 100万件の数値が入ったリストを
- 線形探索すると最大100万ステップかかるが」」「
- 二分探索ではステップ数が対数的に増加しないため、20ステップですむ
- 二分探索では、リストを半分にしていくため、100万件を調べるには 2n = 100万となるnを求めれば、回数がわかる(計算機で2*2=でイコール押し続け、何回目に越えるかでわかる)
- つまり、n = 21ステップで調べることが出来る
- 200万件だと、21ステップでいける
- もちろん、ソート済みが前提であるが、ソートされてないデータだとしても、一度ソートしておけば効率的な場合もある
- 二分探索のPythonのライブラリでは「
bisect」になる
bisect
- 挙動に気をつける
- リストにない場合も、本来あるべきインデックス番号を返してくる
- また、その戻り値がリスト外のときもある
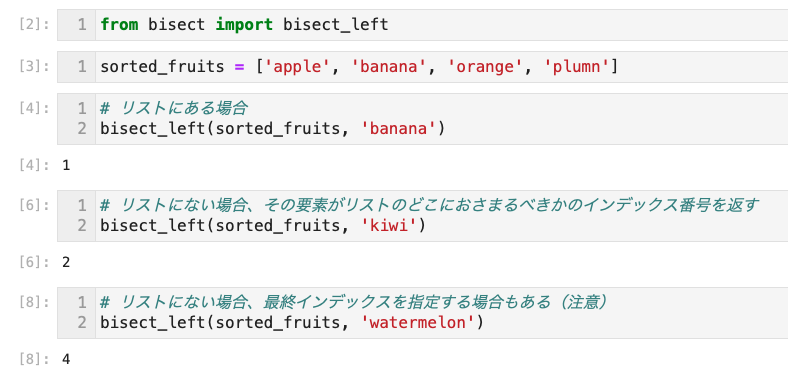
from bisect import bisect_left
def binary_search(an_iterable, target):
index = bisect_left(an_iterable, target)
# bisect_leftの場合、リストにない場合も戻り値がある(本来あるべき場所のインデックス番号)
# またそれがリスト外となる場合、IndexErrorになるため例外処理を追加する
try:
if an_iterable[index] == target:
return True
except IndexError:
return False
else:
return Falsefrom bisect import bisect_left
def binary_search(an_iterable, target):
index = bisect_left(an_iterable, target)
try:
if an_iterable[index] == target:
return print(f'ヒットした行:{index}')
except IndexError:
return False
else:
return False
文字の探索
- 割愛
探索効率と準備コスト
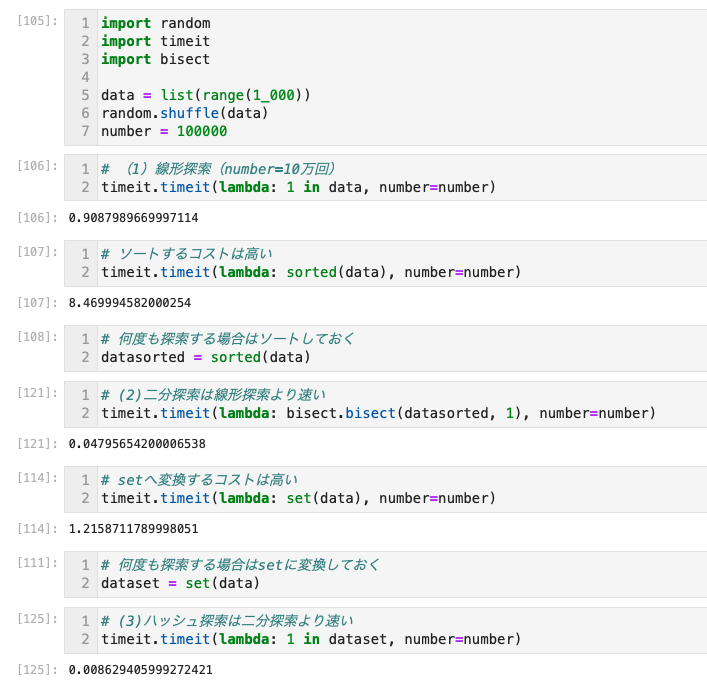
- Pythonにおいて
listに対するinは線形探索setに対するinはハッシュ探索- アルゴリズムとデータ構造の知識があれば、Pythonの
listとsetのどちらがデータ探索に適したデータ型なのかを判断できる(で、どっち?) - ただし、効率の良いアルゴリズムを使うためだとしても、list型を探索のためにソートしたりsetに変換する準備をするのは非効率
- 1回の探索のためであれば、変換コストをかけるよりも線形探索を行うほうが効率の良い場合もある
- 以下で探索やソートがそれぞれどれくらい処理に時間がかかるかを見ていく